

A mixed number should have only a proper fraction and a whole number. If the partner of your whole number is an improper fraction, then you need to convert the improper fraction into mixed numbers and combine the whole numbers. Mixed numbers must have only a whole number and a proper fraction. 7 However, there are some problems in which after adding proper fractions, the result will be an improper fraction. Add the proper fractions and then the whole numbers. The easiest way to add mixed numbers is to add them according to our procedure. We will follow the same steps.Įxample no. This time, we are going to add a proper fraction and an improper fraction. 5 Let’s take a look at another example of adding similar fractions. 4 The same procedure will be applied when adding improper fractions with the same denominator.Įxample no.
Since 4/5 is already the lowest term, then 4/5 is our final answer.Įxample no.2 Let us try to add more proper fractions.Įxample no. Step 5 is to convert our answer into its lowest term. Since we do not have mixed numbers, then we can skip this step. All the denominators are the same 5 thus we can proceed to step 2. Convert your answer into its lowest term or mixed numbers.ĭo you want examples? We will be giving you various examples for you to understand it better.Įxample no.1 This is how we add proper fractions with the same denominators. Add all the whole numbers if it is mixed numbers.

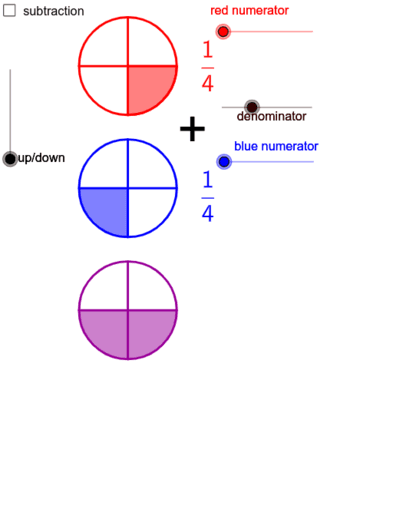
This will be the denominator of our answer. The sum will be the numerator of our answer. Step 1: Ensure that all denominators are the same.
#Add and subtract fractions calculator how to
The following are the steps on how to add similar fractions: How to Add Similar Fractions (the same denominators)Īs a review, similar fractions (also like fractions) are fractions having the same denominators. It will be followed by various examples for you to understand it better. In this lesson, I will be presenting the basic procedure (step-by-step) on how to add or subtract similar fractions. For those who want to review, check my post entitled “Types of Fractions”. I have already discussed similar and dissimilar fraction in my previous post. If we are dealing with denominators, this means that we are dealing with both similar fractions (also called as like fractions) and dissimilar fractions (or unlike fractions). The denominators will tell us if we can add or subtract them directly. After identifying that all denominators were the same, the rest will just be an ordinary addition or subtraction of our numerators. Step 2:Now, multiply the numerator and denominators of both fractions to each other.Īdd fractions calculator can accomplish all of the above performed operations on fractions.Addition and subtraction of similar fractions is nothing but the usual arithmetic operation. Step 1:Reverse the second fraction by interchanging the position of numerator and denominator. Step 1:Multiply the numerator and denominators of both fractions to each other. Step 2: Add the numerator of both fractions and write the denominator by taking it common.īy subtracting the numerators in the end, you can subtract fractions in the same way. Step 1:Make the denominator of both fractions same. This calculator for fractions or fraction solver performs all of the following operations.Įxample:Perform addition, subtraction, multiplication and division on given fraction.Ģ/3 and 3/4 How to add/subtract fractions? The upper part of fraction is known as numerator while the lower part of fraction is known as denominator. When we divide something in parts, a fraction shows the number of parts we have out of total quantity.įor example: If a pizza have total of 8 slices then 1 slice out of 8 can be expressed in fraction as 1/8. What is a fraction?įractions are used to represent part of a whole. Let’s dive into fractions by exploring fraction definition, how to simplify fractions without fraction simplifier, and how do you subtract, add, multiply, or divide fractions manually. Fractions calculator takes the fractions from users and performs the following operations.


 0 kommentar(er)
0 kommentar(er)
